Простой расчет индекса рентабельности инвестиций по формулам PI и ROI

Одним из важнейших критериев определения прибыльности предприятия служит индекс рентабельности. Методам его вычисления посвящена данная статья.

Что такое индекс рентабельности

В названии этого показателя кроется его сущность. Оценка целесообразности инвестирования в тот или иной проект должна производиться на основе расчёта, и чем проще критерий принятия решения, тем легче владельцу капитала сделать выбор. В общем и целом, вопрос состоит в том, стоит ли вкладывать средства в предприятие.

Индекс рентабельности инвестиций – это цифра, показывающая, во сколько раз увеличится покупательская способность вложенных средств за заданный период.

Этот оценочный показатель в ряду многих других по праву считается самым простым и наглядным. Его ценность в том, что он не зависит от многих факторов, оказывающих влияние на оценку возможности и целесообразности инвестирования, в том числе от:

• Размера вкладываемой суммы;
• Общей стоимости проекта;
• Периода инвестирования;
• Направления хозяйственной деятельности;
• Личных качеств инвестора.

Иными словами, вложить в дело можно 10 тысяч рублей или несколько миллионов, а процент прибыли от этого не изменится и будет пропорционален этой сумме.

Использование индекса рентабельности универсально: им можно аргументировать привлечение средств крупных инвесторов или же применять при краудфандинге, когда финансирование проекта осуществляется «народной копейкой».

В обобщённом виде формула индекса рентабельности (IR) выглядит как отношение дисконтированной суммарной стоимости прогнозируемых финансовых поступлений к стоимости всего проекта:

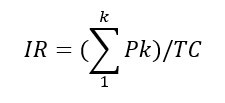
Где:
IR – Индекс рентабельности;
k – Количество денежных потоков (выплат в пользу инвестора);
Pk – Отдельный денежный поток;
TC – Оценочная стоимость проекта.

Это выражение максимально упрощено с целью облегчения понимания и содержит в себе допущение того, что инвестор один, и вся прибыль от вложения достаётся только ему. На практике же всё бывает намного сложнее. Важность IR в том, что он позволяет оценивать доходность вложений в предприятие, абстрагируясь от многих (но не всех) подробностей.

Дисконтирование

Выражение «дисконтированная суммарная стоимость прогнозируемых финансовых поступлений» может кого-то озадачить своей сложностью, но на деле его довольно просто разъяснить. Дело в том, что «лишних денег» в природе современных финансовых отношений практически не бывает. Для того, чтобы инвестировать какую-то сумму в проект, её нужно откуда-то отвлечь, то есть изъять из оборота, приносящего определённый доход. При этом новый индекс рентабельности должен превышать старый (иначе в этих действиях не будет экономической целесообразности). Дисконтирование – это приведение получаемых в результате инвестирования денег в соответствие с актуальной ситуацией.

Возможно, что и сейчас не всё понятно, но пример позволит внести ясность:

Средства, выделенные на инвестирование проекта, лежат на депозитном счёте с начисляемой годовой ставкой в 10%. В данном случае есть возможность применения самого простого способа определения коэффициента дисконтирования – принять его равным банковскому проценту. Он тоже будет учитываться в размере 10%.

Индекс рентабельности инвестиций PI

Существует определённая путаница в трактовке двух показателей, в сущности имеющих один и тот же экономический смысл. При оценке доходности уже работающих предприятий, как правило, используют индекс рентабельности IR, он же ROI (Return Of Investment – переводится как «возвратность инвестиций»). В процессе прогнозирования будущей вероятной прибыли чаще применяют аббревиатуру PI (Profitability Index – «индекс прибыльности»).

Смысловое значение обоих коэффициентов сходное, но в первом случае рассчитывается фактическая величина, а во втором имеет место научно обоснованное предсказание рентабельности после того, как деньги будут вложены в дело. Почти полная тождественность понятий очевидна:

Где:
PI — Индекс прибыльности;
N – Приведенный (дисконтированный) возврат инвестиции в денежном выражении;
I – Дисконтированная сумма инвестиции.

На практике процесс инвестирования чаще всего носит не единовременный, а поэтапный характер. Как правило, в получении сразу всей суммы, необходимой на реализацию проекта, нет необходимости. Деньги предоставляют постепенно, по мере освоения капитала.

Расчёт дисконтированного возврата

При долговременном и поэтапном инвестировании (когда вложения и возвраты осуществляется траншами) показатель N рассчитывается по формуле:

Где:
N – Дисконтированный возврат;
k – Количество выплат (периодов возврата);
T – Время инвестиции, выраженное в годах;
Fk – Периодический денежный поток («порция» возврата за единицу времени, обычно – год);
r – Норма дисконтирования.

Расчёт дисконтированной инвестиции

Не только числитель, но и знаменатель дроби подлежит дисконтированию. Это связано с временными разрывами между траншами, в течение которых деньги продолжают, с одной стороны, терять свою покупательную способность, а с другой же – «работают» на владельца капитала, будучи размещёнными в других местах (к примеру, на банковских счетах).

В связи с этим обстоятельством, формула расчёта приведенной суммы инвестиции также усложняется:

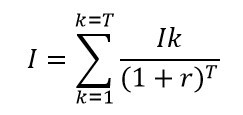
Где:
I – Дисконтированная инвестиция;
k – Количество выплат (периодов возврата);
T – Время инвестиции, выраженное в годах;
Ik — сумма инвестиций в k году;
r – Норма дисконтирования.

Теперь для определения индекса рентабельности инвестиций PI остаётся рассчитать величины N и I по отдельности и поделить одну цифру на другую. Можно, конечно, свести обе составляющие в одно математическое выражение, но тогда формула получится излишне громоздкой и трудной для восприятия.

Пример расчёта IR

Для иллюстрации приведенного выше теоретического материала, целесообразно рассмотреть пример расчета коэффициента рентабельности инвестиции. Ради удобства восприятия исходные данные и результаты вычислений сведены в одну таблицу.

Допустим, что некий инвестор сразу (одним траншем) вложил в проект 150 тыс. руб., и в течение последующих пяти лет, характеризуемых разными ставками дисконтирования, получал выплаты, сначала меньшие, а затем растущие (так на практике обычно и бывает). Задача состоит в определении прибыльности финансирования предприятия.

	Вложенные суммы	Инвестиционный период по годам					Итого
		1	2	3	4	5
Сумма первоначальной инвестиции	150000
Возвраты инвестору по годам		20000	25000	35000	43000	45000	168000
Ставка дисконтирования		1,1	1,05	1,07	1,08	1,04
Дисконтированные денежные потоки	160200	22000	26250	37450	46440	46800	178940

Приведенная сумма инвестирования 160200 руб. получилась в результате умножения начального вложения (150 000 руб.) на среднее арифметическое значение ставок дисконтирования по пяти годам:

(1,1 + 1,05 + 1,07 + 1,08 + 1,04) / 5 = 1,068

Далее:

150000 х 1,068 = 160200

Коэффициент рентабельности инвестиции получается при делении общих приведенных значений денежных поступлений на сумму дисконтированных выплат:

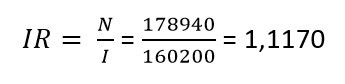
Где:
IR – Индекс прибыльности;
N – Приведенный (дисконтированный) возврат инвестиции в денежном выражении;
I – Дисконтированная сумма инвестиции.

Это означает, что каждый вложенный в проект рубль принёс инвестору 11,7 копеек чистого дохода.

Кроме этого, значение IR, превышающее единицу, свидетельствует об общей прибыльности инвестиции.

Выводы

Рентабельность инвестиции определяется посредством коэффициентов PI и ROI (IR), рассчитываемых по похожим формулам и имеющих сходный экономический смысл.

Показатели индекса прибыльности или рентабельности (возвратности) инвестиций вычисляются на основе дисконтированных (приведенных) сумм денежных потоков и вложений, путём деления одной величины на другую.

Если PI или IR принимают значение менее единицы, инвестиция не может считаться рентабельной.

Значение индекса рентабельности не зависит от суммы инвестирования.

# Бизнес-словарь

Что такое конкуренция

# Бизнес-словарь

Что такое бизнес